Sensitivity, Specificity, Predictive Values and Likelihood Ratios for Dummies

Statistics is one of the most confusing topics for physios and physio students. Most probably this is due to the fact that we care more about people and health than we care about math, right?

Well, I get that you are more interested in assessing your patient properly, good handling, and the latest treatment methods, but I gotta tell you that you need to know the statistical values of a special test and even numbers about prevalence, pre-test, and post-test probabilities of questions you ask your patients during your whole anamnestic process!
I would even dare to say that without the knowledge of the above-mentioned numbers, you will have no clue how much value you can put on certain questions you ask your patient (and the answers thereof) and you will perform special tests without really knowing what a positive or negative outcome will tell you.
When I see or hear that a physio performs a special test like the Thessaly test for meniscus lesions, it is positive, and they are 100% sure afterward, that their patient has a meniscus lesion, it makes me cringe!
PLEASE STOP DOING THAT!
That´s why I urge you to continue reading my post in which I will try to give you an insight into how you can and should use statistics to become a better physio and how that knowledge increases your awareness of your clinical reasoning process!
In general, you will start with your screening, then your anamnesis, followed by a basic assessment. On the basis of the information you got during the aforementioned parts, you are forming your hypotheses that you would either like to confirm or reject. This is where sensitivity and specificity come into play. So let´s first have a look at what sensitivity and specificity are! The easiest way is to watch the short video we have made a while ago:
So to sum it up again: A negative outcome in a 100% sensitive test can rule out the disease (SnNOut) and a positive outcome in a 100% specific test can rule in the disease (SpPIn).
A negative outcome in a 100% sensitive test can rule out the disease (SnNOut) and a positive outcome in a 100% specific test can rule in the disease (SpPIn)
With the two mnemonics SnNOut and SpPIn, it´s relatively easy to put these two concepts into practice.
Most of the time, you will get a better grasp on their definition and what they actually are if you are able to calculate these values using a 2×2 table. Watch our next video, which will show you how to do the calculation part:
Unfortunately, in real life, there are hardly any 100% accurate tests, which is why you will have a lot of false-positive and false-negative results. On top of that, sensitivity and specificity tell us how often a test is positive in patients who we already know have the disease or not. In practice, we however do not know whether our patients have a certain condition or not. What we rather do in practice is to interpret the results of a positive or negative test.
You usually won’t know what the probability is that the patient actually has the disease with a positive outcome and how high the probability is that a patient does not have the disease with a negative outcome.
These values are called positive predictive value (PPV) and negative predictive value (NPV), also called post-test probabilities. You guessed it – we have another video that explains these values with the help of the 2×2 table and shows you how to calculate these values:
Now, as mentioned in the video PPV and NPV are great tools if you have a good idea about the prevalence of your patient group and if this prevalence is identical to the prevalence of the RCT, where you have gotten your statistical values from for a specific test in the first place. If this is not the case, PPV and NPV become pretty much useless.
Imagine how the pre-test probability of an anterior cruciate ligament (ACL) rupture changes in different settings: For example, the prevalence of patients with an ACL tear in a general practice will be much lower than in a sports clinic that is specialized in knee injuries. The higher the prevalence, the higher your PPV and the lower your NPV will be.
Maybe we’ll make a video on that as well in the future, but it´s important to remember that we need a better value than the PPV and NPV, which is where the likelihood ratios come into play.
The likelihood ratio combines both sensitivity and specificity and tells us how likely a given test result is in people with the condition, compared with how likely it is in people without the condition. Watch the following video about likelihood ratios and how you can calculate them:
In the example, we used the Lachman test, which is one of the most accurate tests that are out there in clinical practice but let´s look at our beloved Thessaly test and how our example plays out there:
According to Goossens et al. (2015), the Thessaly test has a sensitivity of 64% and a specificity of 53%, which results in a LR+ of 1,36 and a LR- of 0,68. As you can already see, these values are pretty close to LR = 1, which tells us that they will change the probability that a person has a meniscus lesion very little. To apply these values to the example of our ACL tear case, we know that ACL tears are often accompanied by meniscal tears. Although our patient does not report any locking or catching sensations, we estimate our pre-test probability at about 30%.
Our nomogram will look like this:
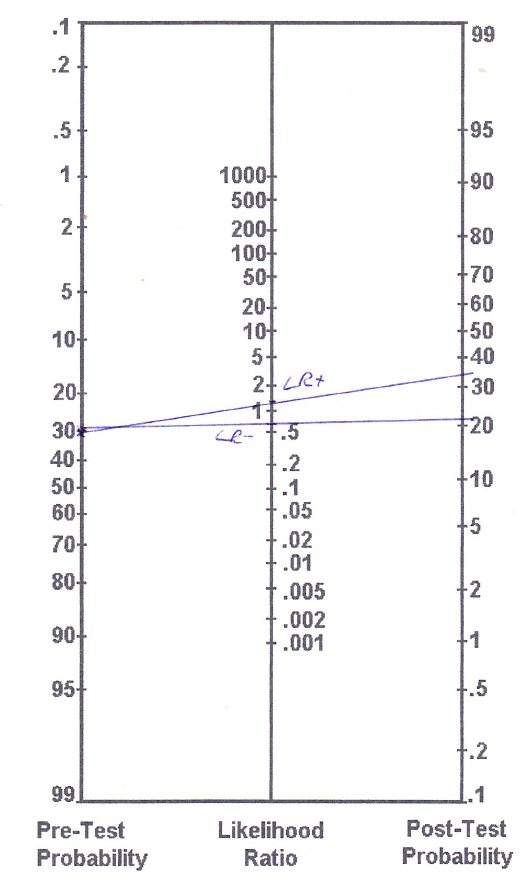
Based on the (more accurate) calculations we end up with the following post-test probabilities:
– Pre-test odds: Prevalence/(1-prevalence) = 0,3/(1-0,3) = 0,43
– Post-test odds (LR+): 0,43 x 1,36 = 0,58
– Post-test probability (LR+): post-test odds / (post-test odds+1) = 0,58/(0,58+1) = 0,37 (so 37%)
– Post-test odds (LR-): 0,43 x 0,68 = 0,29
– Post-test probability (LR-): post-test odds / (post-test odds+1) = 0,29/ (0,29+1) = 0,22 (22%)
So with a positive Thessaly test, you have increased your chances of a mensical lesion from an assumed 30% to 37% and with a negative Thessaly test, you have decreased your chances to 22%.
See why I am freaking out if people perform a test and then they assume that their patient definitely does or does not have a certain condition?! And this is all based on an assumption of the pre-test odds, which most people even forget to take into consideration!
If you want to perform multiple tests, say you want to add the Anterior Drawer test in our ACL example, you will base your pre-test probability on the post-test probability of the Lachman test. So in the case of a positive Lachman, you will start with a pre-test probability of 95%, and with a negative Lachman, you will start with a pre-test probability of 19%.
While most tests either have a positive or negative outcome, there are also test clusters with multiple outcomes. So if you take the cluster of Laslett for example, for 2 out of 5 positive tests you will end up at an LR+ of 2.7, for 3/5 at an LR+ of 4.3, etc.
Be aware though, that with a very high pre-test probability, another test has little value and it is better to start your treatment. The same is true for a very low pre-test probability in which case you don´t test and also do not treat the condition.
As an example, if a patient presents to you with sudden onset of low back pain, neurological symptoms in both legs, problems with micturition and saddle anesthesia, you would be pretty sure that this patient has cauda equina syndrome, which is a red flag and requires urgent surgery. So if you are say 99% sure of your diagnosis, a straight leg test (SLR) with a LR- of 0.2 will decrease the post-test probability to 95%, which is still very high and you would still want to send this patient for surgery.
In turn, if the test was positive, you would probably go from 99% to 100% certainty, so why bother testing in the first place, especially if this is an urgent referral for surgery?
The same is true for a very low pre-test probability. If a patient presents to you without radiating pain below the knee, the chance of this patient for radicular syndrome due to a disc herniation is very low, say we assume 5%. So what would happen in this case if you performed the SLR with a LR+ of 2.0? You would end up at a post-test probability of 10% and if the test is negative the post-test probability would have decreased to maybe 4%. So if you are almost certain, that a patient does not have a certain disease, why test it in the first place?
Of course, in practice, the decision to do a certain test always depends on various factors such as costs, the severity of a disease, risks of the test, etc.
Now let´s get back to what I claimed in the beginning, that statistical values help you to evaluate the outcome of your questioning during your patient-history taking.
In fact, every question can be seen as a special test, in which the answer (yes or no) will either increase or decrease the probability that a patient has a certain condition. This is also the reason why a thorough anamnesis is most of the time more important than special testing because you are basically performing a series of special tests in a row,
if you are a good clinician who knows how to form a hypothesis based on your patient’s answers.
So let´s take another example: How does a positive answer to the question about prolonged use of corticosteroids influence the chance of a spinal fracture?
According to Henschke et al. (2009), prolonged use of corticosteroids has a positive LR+ of 48.5. The prevalence (pre-test probability) of a spinal fracture presenting to primary care can be estimated between 1%-4% according to Williams et al. (2013) in patients who present with low back pain.
So with prolonged corticosteroid use, we will end up with a post-test probability of 33% although we assumed only 1% of prevalence in this example calculation.
I think it´s fair to say that this question about corticosteroids should always be asked in the screening procedure for spinal fractures!
Now let´s take a look at another red flag that is commonly used in the screening for malignancy in patients with low back pain: Insidious onset of low back pain.
According to Deyo et al. (1988, I admit this is a pretty old study), the LR+ for this question is 1.1. According to Henschke et al (2009), the prevalence of malignancy in patients with low back pain is even lower than 1%, but we will calculate with this 1% just for simplicity.
So the red flag insidious onset increases the post-test probability of malignancy as the cause of low back pain from 1% to exactly 1,1%. I think we can agree that this red flag should be kicked out of any guideline in which it is listed.
Orthopedic Physiotherapy of the Upper & Lower Extremities
Boost Your Knowledge about the 23 Most Common Orthopedic Pathologies in Just 40 Hours Without Spending A Fortune on CPD Courses
I know this was a long post and congratulations and respect if you made it here! My goals were to give you an explanation about how to work with statistical values like sensitivity, specificity, PPV, NPV, and especially the likelihood ratios and to make you aware of their importance in your whole physiotherapeutic process.
It would be fantastic if you could take the prevalence of a certain hypothesis into account with your future patients, have an idea about the impact of your anamnestic questions on the pre-test probability, and you could properly evaluate the power of your special testing.

Feel free to ask questions in the comment and to share this blog post if you found it helpful!
Thank you for reading!
Kai
References

Kai Sigel
CEO & Co-Founder Physiotutors
NEW BLOG ARTICLES IN YOUR INBOX
Subscribe now and receive a notification once the latest blog article is published.







